Geometri Dasar

 

Istilah dalam Geometri: Definisi, Postulat, dan Aksioma

Definisi

Definisi adalah kata, frasa, atau kalimat yang mengungkapkan makna, keterangan, atau ciri utama dari orang, benda, proses, atau aktivitas. Definisi dalam geometri tidak perlu dibuktikan lagi. Terdapat 23 jenis definisi yang digunakan dalam geometri dasar, yaitu:

                                         

• Definisi 1: Titik adalah sesuatu yang tidak memiliki bagian (sesuatu yang memiliki posisi tetapi tidak memiliki dimensi). Penamaan titik dalam matematika menggunakan huruf kapital.

• Definisi 2: Garis adalah sesuatu yang memiliki panjang tetapi tidak memiliki lebar. Garis merupakan himpunan dari banyak titik dan dapat dibedakan menjadi dua, yaitu ruas garis yang dibatasi oleh dua ujung berbeda dan sinar garis yang hanya memiliki titik mula dan memili panjang tak hingga.

• Definisi 3: Ujung-ujung suatu garis adalah titik.

• Definisi 4: Garis lurus adalah garis yang terletak secara rata dengan titik-titik pada dirinya.

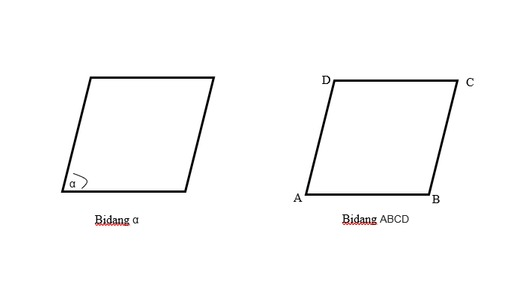
• Definisi 5: Bidang adalah sesuatu yang hanya mempunyai panjang dan lebar.

• Definisi 6: Sisi-sisi dari bidang berupa garis.

• Definisi 7: Bidang datar adalah bidang yang terletak secara rata debgab garis-garis lurus pada dirinya.

• Definisi 8: Suatu bidang terbentuk dari dua garis pada bidang yang bertemu pada sebuah titik dan tidak terletak dalam sebuah garis lurus.

• Definisi 9: Dan ketika garis-garis yang membentuk sudut lurus, sudut tersebut disebut rectilinear

• Definisi 10: Ketika garis lurus berdiri pada sebuah garis lurus dan membentuk sudut yang berdekatan yang besarbta sama, masing-masing sudut tersebut adalah sudut siku-siku, dan garis yang berdiri dikatakan tegak lurus dengan garis lurus tempatnya berdiri.

• Definisi 11: Sudut tumpul adalah sudut yang lebih besar dari sudut siku-siku.

• Definisi 12: Sudut lancip adalah sudut yang lebih kecil dati sudut siku-siku.

• Definisi 13: Batas adalah sesuatu yang merupakan ujung dari apapun.

• Definisi 14: Bangun adalah sesuatu yang dibentuk oleh batas atau batas-batas. Misalnya, garis memiliki batasan berupa titik, bidang memiliki batasan garis, dan bangun ruang memiliki batasan bidang.

• Definisi 15: Lingkaran adalah bangun datar yang dibentuk oleh satu garis sedemikian hingga semua garis lurus yang jatuh pada bangun tersebut dari sebuah titik di dalam bangun tersebut pada bangun tersebut panjangnya sama.

• Definisi 16: Dan titik tersebut disebut pusat lingkaran.

• Definisi 17: Diameter lingkaran adalah suatu garis lurus yang digambar melalui pusat lingkaran dan berakhir di dua arah keliling lingkaran.

• Definisi 18: Setengah lingkaran adalah bangun yang dibangun oleh diameter dari keliling lingkaran yang dipotong oleh diameter.

• Definisi 19: Bangun-bangun rectilinear adalah bangun-bangun yang dibentuk oleh garis lurus. Bangun segitiga adalah bangun yang dibentuk oleh tiga garis lurus, bangun segiempat adalah bangun yang dibentuk oleh empat garis lurus, bangun segibanyak adalah bangun yang dibentuk oleh lebih dari empat garis lurus.

• Definisi 20: Dari bangun segitiga, segitiga sama sisi adalah segitiga yang memiliki tiga sisi yang sama, segitiga sama kaki adalah segitiga yang memiliki dua sisi yang sama, segitiga sembarang (segitiga tak sama panjang) adalah segitiga yang ketiga sisinya tidak ada yang sama.

• Definisi 21: Selanjutnya, pada bangun segitiga, segitiga siku-siku adalah segitiga yang memiliki sudut siku-siku, segitiga tumpul adalah segitiga yang memiliki sudut tumpul, segitiga lancip adalah segitiga yang memiliki sudut lancip.

• Definisi 22: Pada bangun segiempat, persegi adalah bangun yang semua sisinya memiliki panjang yang sama dan memiliki sudut siku-siku, persegi panjang adalah bangun yang memiliki sudut siku-siku tetapi tidak emmiliki dua pasang sisi yang panjangnya sama,belah ketupat adalah bangun yang semua panjang sisinya sama tetapi tidak memiliki sudut siku-siku.

• Definisi 23: Garis-garis lurus sejajar adalah garis lurus yang berada pada bidang datar yang sama, dan jika diperpanjang secara terus menerus pada kedua arah tidak akan berpotongan di arah manapun.

Postulat

Postulat adalah asumsi yang menjadi pangkal dalil yang dianggap benar tanpa perlu membuktikannya, anggapan dasar untuk satu ilmu tertentu. Dalam geometri dasar, terdapat 5 jenis postulat yaitu:

• Postulat 1: Melalui dua titik sebarang dapat dibuat garis lurus.

• Postulat 2: Ruas garis dapat diperpanjang secara kontinu menjadi garis lurus.

• Postulat 3: Melalui sebarang titik dan sebarang jarak dapat dilukis lingkaran.

• Postulat 4: Semua sudut siku-siku sana.

• Postulat 5: Jika suatu garis memotong dua garis lurus dan membuat sudut-sufut dalam sepihak kurang dari dua sudut siku-siku, kedua garis tersebut jika diperpanjang tak terbatas, akan bertemu dipihak tempat kedua sudut dalam sepihak kurang dari dua sudut siku-siku.

Aksioma

Aksioma adalah pendapat yang dijadikan pedoman dasar dan merupakan dalil pemula, kebenarannya tidak perlu dibukktikan lagi atau aksioma yaitu suatu pernyataan yang diterima sebagai kebenaran dan bersifat umum untuk semua cabang ilmu tanpa memerlukan pembuktian. Dalam geometri, terdapat 5 jenis aksioma yaitu:

• Aksioma 1: Hal-hal yang sama adalah sama dengan suatu yang lain.

Contoh, A = B dan B = A

• Aksioma 2: Jika sesuatu yang sama ditambah dengan sesuatu yang sama, jumlahnya sama.

Contoh, jika A = B, maka A + C = B + D

• Aksioma 3: Jika sesuatu yang sama dikurangi dengan sesuatu yang sama, jumlahnya sama.

Contoh, jika A = B, maka A - C = B - D

• Aksioma 4: Hal=hal yang berimpit satu sama lain, hal-hal tersebut sama.

• Aksioma 5: Keseluruhan lebih besar dari pada sebagian.