Teori Bilangan

 

Silsilah Bilangan

    Bilangan adalah suatu konsep matematika yang digunakan dalam pencacahan dan pengukuran. Simbol ataupun lambang yang digunakan untuk mewakili suatu bilangan disebut sebagai angka atau lambang bilangan. Sedangkan nomor menujukkan kedudukan dalam urutan. Jadi, bilangan, angka, dan nomor ialah tiga hal yang berbeda namun berhubungan satu sama lain dalam matematika.

        Bilangan yang umum diketahui yakni bilangan bulat yang dimulai dari 0 dan seterusnya. Akan tetapi, terdapat silsilah yang dapat menghasilkan bilangan bulat serta jenis bilangan lainnya. Adapun silsilah bilangan dan penjelasannya sebagai berikut:

1. Bilangan Kompleks

Bilangan kompleks mencakup keseluruhan bilangan yang dinotasikan dengan 'a+bi', dimana a dan b ialah bilangan rill dan i adalah bilangan imajiner (√-1). Bilangan kompleks dapat dibedakan menjadi bilangan imajiner dan bilangan real/rill.

Contoh: 2+3i, 9-5i, dll.

2. Bilangan Imajiner

Bilangan imajiner atau bilangan khayal ialah bilangan real/rill yang dikalikan dengan unsur imajiner. Bilangan imajiner dinotasikan dengan 'i', dimana i2=-1. Bilangan imajiner tidak dapat dibagi menjadi bilangan lainnya.

3. Bilangan Real/Rill

Bilangan real atau bilangan riil adalah bilangan yang digunakan untuk mengukur kuantitas seperti jarak, durasi atau suhu. Bilangan real/rill terdiri atas bilangan irasional dan bilangan rasional. Himpunan bilangan real/rill dapat dinotasikan dengan '{R}'.

Contoh: 0, 2, 7/11, √2, dll.

4. Bilangan Irasional

Bilangan irasional adalah bagian dari bilangan real/rill yang tidak dapat dibagi dan tidak dapat dinyatakan dalam bentuk pecahan a/b, dengan a dan b adalah bilangan bulat serta b tidak sama dengan nol. Bilangan irasional juga tidak memiliki pengulangan pola.

Contoh: √2, √31, dll.

5. Bilangan Rasional

Bilangan rasional merupakan kebalikan dari bilangan irasional, yakni bilangan yang dapat dinyatakan dalam bentuk pecahan dan memiliki pengulangan pola. Bilangan rasional dapat berupa bilangan bulat atau pecahan yang merupakan bagian dari bilangan rasional.

Contoh: 4/2, 9/3, 1/20, dll.

6. Bilangan Pecahan

Bilangan pecahan ialah bagian bilangan rasional yang bernotasi 'a/b', dimana a dan b adalah bilangan bulat dan b tidak sama dengan nol. Kemudian a dapat disebut dengan pembilang dan b adalah penyebut suatu pecahan.

• Jika penyebut pecahan membagi habis suatu pembilang, maka disebut dengan pecahan biasa/murni.
• Jika penyebut tidak membagi habis pembilang, maka disebut dengan pecahan campuran.
• Jika penyebut lebih kecil dan membagi habis pembilang, maka disebut dengan pecahan desimal.

Contoh: 4/2 (pecahan biasa), 11/2 (pecahan campuran) 1/4 (pecahan desimal), dll.

7. Bilangan Bulat

Bilangan bulat ialah bilangan yang sering digunakan dalam kehidupan sehari-hari. Bilangan bulat terdiri dari bilangan bulat negatif dan bilangan cacah, maka dari itu himpunan dari bilangan bulat dimulai dari negatif tak hingga sampai positif tak hingga.

Contoh: -8, 0, 34, dll.

8. Bilangan Bulat Negatif

Bilangan bulat negatif adalah bagian bilangan bulat yang bernilai negatif atau memiliki notasi '-' pada depan angka. Nilai untuk bilangan bulat negatif sendiri pastinya kurang dari nol (x<0).

Contoh: -11, -86, -145, dll.

9. Bilangan Cacah

Bilangan cacah adalah bilangan yang dimulai dari nol sampai tak hingga. Bilangan cacah dapat dibagi menjadi bilangan nol dan bilangan asli.

Contoh: 0, 100, 375, dll.

10. Bilangan Nol

Bilangan nol sebenarnya adalah angka kosong karena digunakan untuk melambangi sesuatu yang kosong atau tidak memiliki nilai. Jadi, bilangan nol tidak memiliki nilai apapun melainkan sebagai identitas bagi bilangan lainnya. Contoh dari bilangan nol hanyalah 0 atau bilangan itu sendiri.

11. Bilangan Asli

Bilangan asli dapat pula disebut dengan bilangan bulat positif. Bilangan asli sering digunakan pula untuk menghitung dalam kegiatan sehari-hari. Akan tetapi, bilangan asli tidak lagi menyertakan nol di dalamnya, sehingga bilangan asli dimulai dari 1 sampai positif tak hingga. Bilangan asli dapat dibagi menjadi beberapa bilangan lainnya seperti bilangan ganjil, bilangan genap, bilangan prima, dan bilangan komposit.

Contoh: 1, 4, 908, dll.

12. Bilangan Genap

Bilangan genap ialah bagian bilangan asli yang habis dibagi dua. Bilangan genap dimulai dari 2 dan berlaku dengan kelipatannya yakni setiap dua angka setelahnya. Bilangan genap dapat dirumuskan dengan '2n'.

Contoh: 4, 6, 8, dll.

13. Bilangan Ganjil

Bilangan ganjil ialah bagian bilangan asli yang tidak habis jika dibagi dua. Bilangan ganjil dimulai dari 1 dan memiliki pengulangan setiap dua angka setelahnya, sehingga bilangan ganjil dapat dirumuskan dengan '2n+1'.

Contoh: 3, 5, 7, dll.

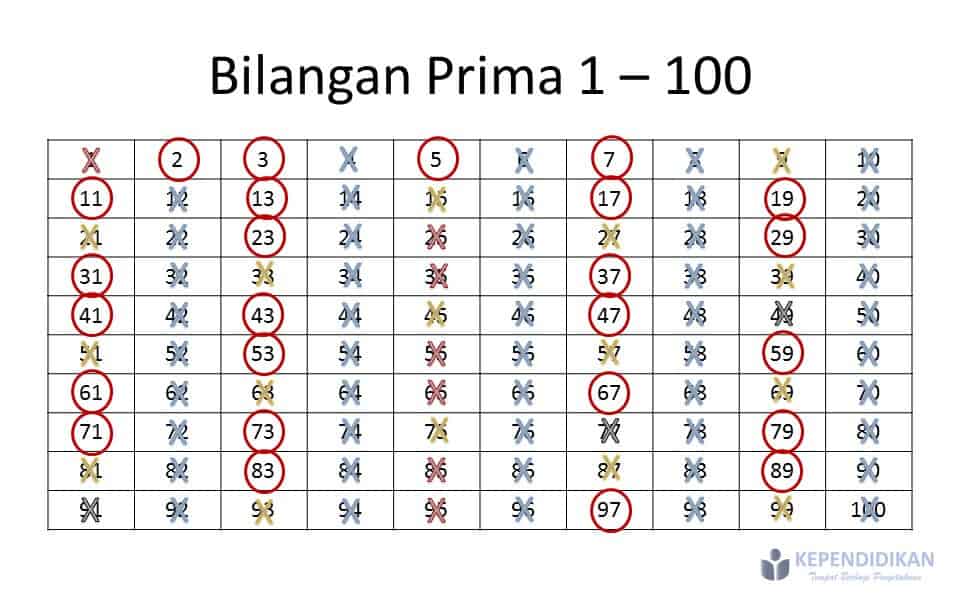
13. Bilangan Prima

Bilangan prima ialah bilangan asli yang hanya memiliki dua faktor, yaitu angka 1 dan angka itu sendiri. Bilangan prima dimulai dari angka 1. Adapun cara menentukan bilangan prima sebagai berikut:

• Tuliskan angka mulai dari 1 hingga seterusnya, kemudian perhatikan dimulai angka terkecil dahulu.
• Angka 1 bukanlah bilangan prima karena tidak ada angka lain yang dapat membaginya, maka coret/silang angka tersebut.
• Angka 2 dapat dibagi dengan 1 dan 2, yang mana sudah memenuhi syarat bilangan prima, maka coret/silang kelipatan dari angka tersebut (angka genap).
• Angka 3 dapat dibagi dengan 1 dan 3, yang mana sudah memenuhi syarat bilangan prima, maka coret/silang kelipatan dari angka tersebut.
• Lakukan hal yang sama kepada angka lainnya hingga tidak ada lagi bilangan lain yang memiliki lebih dari dua faktor. Bilangan yang tidak dicoret/silang ialah himpunan bilangan prima.

Contoh: 2, 7, 13, dll.

14. Bilangan Komposit

Bilangan komposit adalah kebalikan dari bilangan prima, yaitu bilangan yang memiliki lebih dari dua faktor. Bilangan komposit juga dapat dikatakan sebagai bukan bilangan prima. Jadi, angka yang tercoret/silang saat penentuan bilangan prima merupakan bilangan komposit.

Contoh: 4, 6, 12, dll.